【RL】PPO算法入门#

强化学习（Reinforcement Learning, RL）在机器人领域的应用本质上都是为了解决一个核心问题：让机器人通过与环境的交互，自主学习到一个最优的策略（Policy），从而完成特定任务。这些方法都满足一个基本的框架：

感知（Perception）: 机器人通过传感器感知当前环境的状态 $s_t$ 。
决策（Decision）: 机器人的策略 $\pi$ 根据当前状态 $s_t$ 决定要执行的动作 $a_t$ 。
行动（Action）: 机器人执行动作 $a_t$ ，与环境发生交互。
学习（Learning）: 环境根据机器人的动作反馈一个新的状态 $s_{t+1}$ 和一个奖励信号 $r_t$ 。算法利用这个反馈信息 $(s_t, a_t, r_t, s_{t+1})$ 来更新和优化策略 $\pi$ 。

从数学原理上讲，所有这些强化学习方案的共同基础是马尔可夫决策过程（Markov Decision Process, MDP）

在上图中，机器人通过感知环境，获取状态，通过Actor中的策略 $\pi$ 输出对应的行动与环境进行交互，进而状态改变。不断重复上述过程，直到任务结束，这样就得到了一个由不同时刻Actor的输入与输出组成的序列 $\tau$ 。

PG（Policy Gradient）#

策略梯度算法（Policy Gradient, PG）则是将其看作一个基于参数 $\theta$ 随机策略 $\pi_\theta$ ，通过寻找一个最优策略并最大化这个策略在环境中的期望回报：

\pi_\theta^*=\arg \max_\theta J(\theta) = \arg \max_\theta\mathbb{E}_{s_0}\left[V^{\pi_\theta}(s_0)\right] = \arg \max_\theta \mathbb{E}_{\pi_\theta}\left[\sum^{\infty}_{t=0}r(s_t, a_t)\right]\tag{1}

对于我们要训练的一个任务而言，初始的时候，由于Actor会在不同的state做出怎样的action是不确定的，因此发生序列 $\tau$ 的概率分布为：

\begin{aligned} p_{\theta}(\tau) &= p(s_1)p_{\theta}(a_1|s_1)p(s_2|s_1,a_1)p_{\theta}(a_2|s_2)p(s_3|s_2,a_2)\cdots \\ &= p(s_1)\prod_{t=1}^{T} p_{\theta}(a_t|s_t)p(s_{t+1}|s_t,a_t) \end{aligned}

由上，我们就可以得到在序列 $\tau$ 下，以 $\theta$ 为参数的策略获得的累计奖励（这里的累计奖励就是 (1) 中的价值函数）为：

J(\theta) = \mathbb{E}_{\tau\sim p_\theta(\tau)}\left[ R(\tau) \right] = \sum_\tau R(\tau)p_\theta(\tau)

其中， $\mathbb{E}_{\tau \sim p_\theta(\tau)}$ 的含义为在在策略 $\pi_\theta$ 下，轨迹 $\tau$ 按照分布 $p_\theta(\tau)$ 随机产生的期望。要求 $J(\theta)$ 的极大值，可以通过梯度上升法进行求解，也就需要求解 $\nabla_\theta J(\theta)$ 。

\nabla_\theta J(\theta) = \sum_{\tau} R(\tau) \nabla p_\theta(\tau)

对上式而言，并不能直接求和，因为 $p_\theta(\tau)$ 过于庞大，因此需要对上式进行一些化简：

\nabla_\theta J(\theta) = \sum_{\tau} R(\tau) p_\theta(\tau) \frac{\nabla p_\theta(\tau)}{p_\theta(\tau)}

由链式法则我们有：

\sum_{\tau} R(\tau) p_\theta(\tau) \frac{\nabla p_\theta(\tau)}{p_\theta(\tau)} = \sum_{\tau} R(\tau) p_\theta(\tau) \nabla \log p_\theta(\tau)

显然有 $\sum_\tau p_\theta(\tau) = 1$ ，因此有：

\sum_{\tau} R(\tau) p_\theta(\tau) \nabla \log p_\theta(\tau) = \mathbb{E}_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla \log p_\theta(\tau)]

进而可以对上式进行数值求解（Monte Carlo method）：

\begin{aligned} \mathbb{E}_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla \log p_\theta(\tau)] &\approx \frac{1}{N} \sum_{n=1}^{N} R(\tau^n) \nabla \log p_\theta(\tau^n) \\ &=\frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} R(\tau^n) \nabla \log p_\theta(a_t^n | s_t^n) \end{aligned}

就可以通过实际采集的样本求解目标函数 $J(\theta)$ 的梯度。

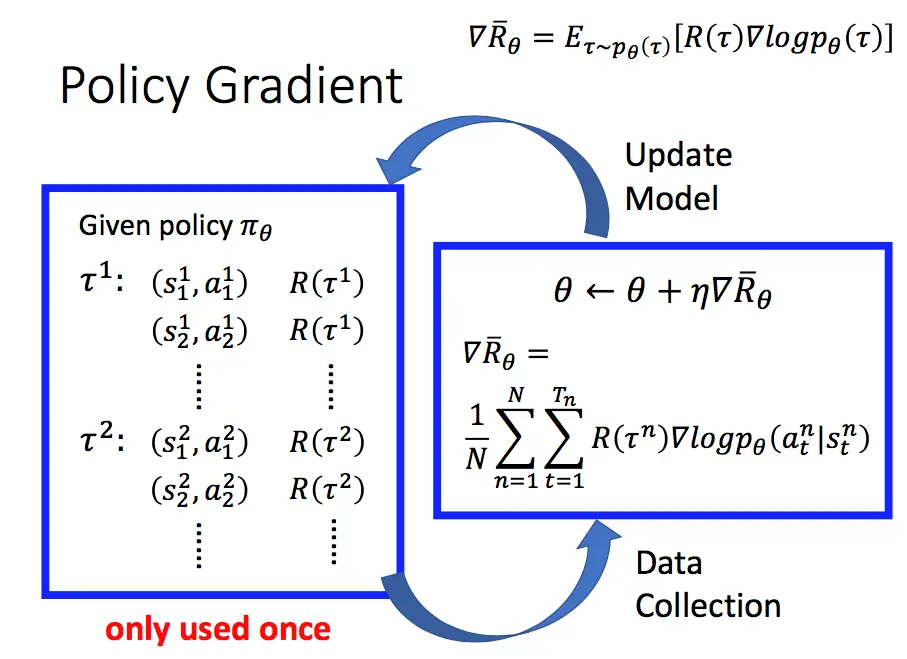
从上述流程图中不难看出，采集到的数据都是当前策略与环境之间交互的结果。因此策略梯度算法是一种在线策略（on-policy）算法，需要根据当前采样的数据来计算梯度。在线策略需要每迭代一步就重新采集数据，这样的训练无论是从时间还是内存上都是巨大的消耗，因此我们需要考虑如何才能让模型能反复从一组采样数据上学习 $\theta'$ 另 $J(\theta') > J(\theta)$ 。

TRPO (Trust Region Policy Optimization)#

由于初始状态 $s_0$ 的分布和策略无关，因此上述策略 $\pi_\theta$ 下的优化目标 $J(\theta)$ 可以写成在新策略 $\pi_{\theta'}$ 的期望形式：

\begin{aligned} J(\theta) &= \mathbb{E}_{s_0}\left[V^{\pi_\theta}(s_0)\right] = \mathbb{E}_{\pi_{\theta'}}\left[\sum^\infty_{t = 0}\gamma^tV^{\pi_\theta}(s_t) - \sum^\infty_{t = 1}\gamma^tV^{\pi_\theta}(s_t) \right]\\ &=-\mathbb{E}_{\pi_{\theta'}}\left[\sum^\infty_{t = 0}\gamma^t(V^{\pi_\theta}(s_{t+1}) -V^{\pi_\theta}(s_t)) \right] \end{aligned}

对两个参数之间的目标函数做差可得（具体推导过程见TRPO单调性证明）：

\begin{aligned} J(\theta') - J(\theta) &= \mathbb{E}_{s_0} \left[ V^{\pi_{\theta'}}(s_0) \right] - \mathbb{E}_{s_0} \left[ V^{\pi_\theta}(s_0) \right]\\ &= \mathbb{E}_{\pi_{\theta'}} \left[ \sum_{t=0}^{\infty} \gamma^t r(s_t, a_t) \right] + \mathbb{E}_{\pi_{\theta'}} \left[ \sum_{t=0}^{\infty} \gamma^t \left( \gamma V^{\pi_\theta}(s_{t+1}) - V^{\pi_\theta}(s_t) \right) \right]\\ &= \mathbb{E}_{\pi_{\theta'}} \left[ \sum_{t=0}^{\infty} \gamma^t \left( r(s_t, a_t) + \gamma V^{\pi_\theta}(s_{t+1}) - V^{\pi_\theta}(s_t) \right) \right]\\ &= \mathbb{E}_{\pi_{\theta'}} \left[ \sum_{t=0}^{\infty} \gamma^t A^{\pi_\theta}(s_t, a_t) \right] \\ &= \frac{1}{1 - \gamma} \mathbb{E}_{s \sim \nu^{\pi_{\theta'}}} \mathbb{E}_{a \sim \pi_{\theta'}(\cdot|s)} \left[ A^{\pi_\theta}(s, a) \right] \end{aligned}

其中 $A^{\pi_\theta}$ 为优势函数（Advantage Function）。上述的式子说明，只要找到的策略满足：

\mathbb{E}_{s \sim \nu^{\pi_{\theta'}}} \mathbb{E}_{a \sim \pi_{\theta'}(\cdot|s)} \left[ A^{\pi_\theta}(s, a) \right] \geq 0

就可以满足 $J(\theta') > J(\theta)$ 。为了求解该式，TRPO选择了使用原策略 $\pi_\theta$ 的状态分布做了近似处理，并使用重要性采样对动作分布进行处理，得到目标函数 $L_\theta(\theta')$ ，并使用KL散步保证这两者之间足够接近。TRPO优化公式如下：

\begin{aligned} &\max_{\theta'}\ L_\theta(\theta') = J(\theta) + \mathbb{E}_{s \sim \nu^{\pi_{\theta}}} \mathbb{E}_{a \sim \pi_{\theta}(\cdot|s)} \left[ \frac{\pi_{\theta'}(a |s)}{\pi_\theta(a|s)} A^{\pi_\theta}(s, a)\right] \\ &\text{s.t. }\quad\mathbb{E}_{s\sim \nu^{\pi_{\theta_k}}}[D_{KL}(\pi_{\theta_k}(\cdot | s), \pi_{\theta'}(\cdot | s))] \leq \delta \end{aligned}

PPO（Proximal Policy Optimization）#

PPO算法与TRPO算法的区别在于对于参数 $\theta$ 的约束。为了模型能从示范分布 $\theta'$ 中学习参数，就必须让我们学习的参数 $\theta$ 与示范数据中的 $\theta'$ （未知）的分布差距不大。TRPO使用KL散度作为约束项来约束优化目标。而PPO算法直接将约束放在优化目标函数上。目前的PPO算法有两种实现方式：近端策略优化惩罚（PPO-penalty）与近端策略优化裁剪（PPO-clip）