KD-Tree#

作为当前空间信息处理绕不开的一个数据结构，KD-Tree因其在处理高维度空间信息的高效性，被广泛使用到各种机器人感知，三维重建，光线追踪算法等领域。当然也衍生了一系列针对该算法的优化方法。这篇文章将从KD-Tree的原理出发，详细谈一谈该算法的原理以及目前的优化策略。

KD-Tree 算法#

KD-Tree（k-Dimension Tree, KDT），是一种具有二叉搜索树形态的特殊的树结构，其中每个结点都对应k维空间中的一个点。每个子树中的点都在一个k维超平面内部，这个超平面也被称为边界框（Bounding Box），例如在二维空间中这个超平面就是一个平面，如下图所示，就是边界的框。

kdt1

建树#

综合比较下来我觉得最普遍的方式可以用OI-Wiki中的概括

假设已有 $k$ 维空间中的 $n$ 个不同点的坐标，要构建一个KD-Tree，步骤如下（递归）：

如果当前超平面中只有一个点，返回。
选择一个维度，将当前超平面按照这个维度分成两个超平面。
选择切割点：在选择的维度上选择一个点，这一维度上的值小于这个点的归入一个超平面（左子树），其余的归入另一个超平面（右子树）。
将选择点作为子树的根节点，递归对分出两个超长方体，构建左右子树，维护子树信息。

以上图为例，构建出的树结构如下：

kdt2

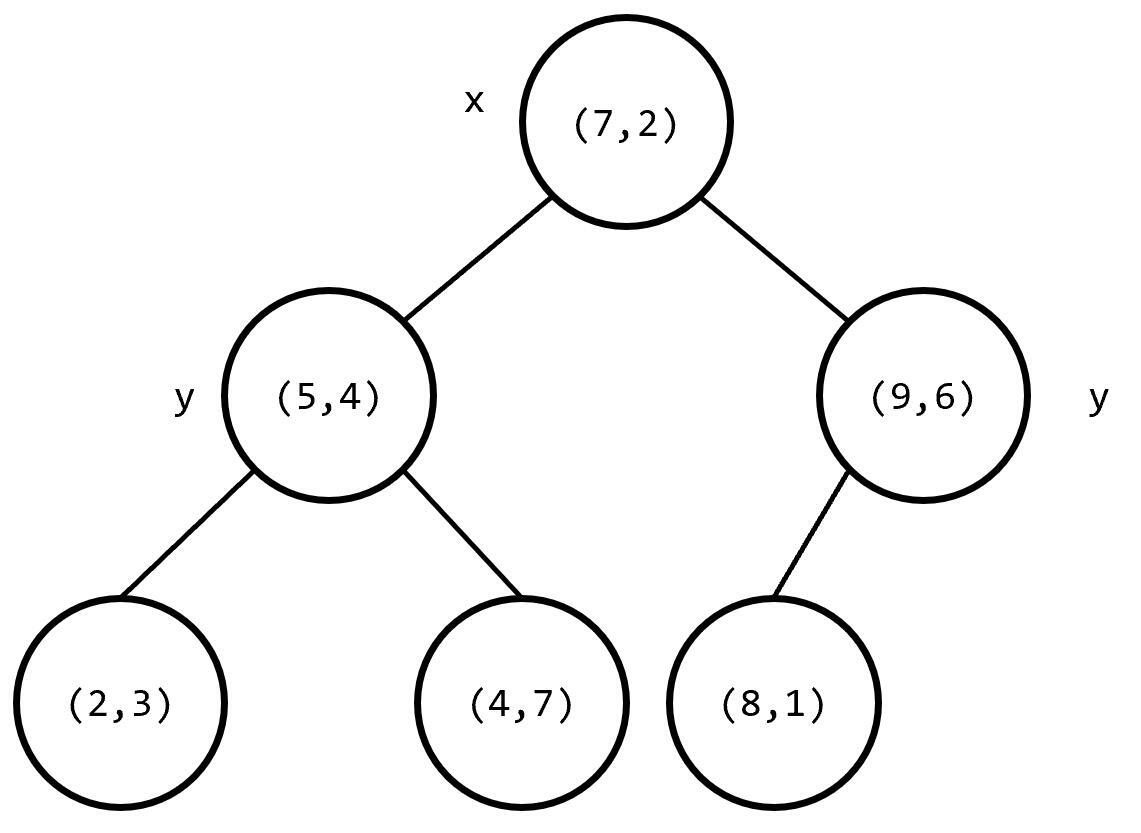
建树过程中最主要的优化方向就是维度与切割点的选择。这两部分的选择直接决定了树的形态。而对于一个树结构来说，越接近平衡二叉树，在空间复杂度与查询时的时间复杂度上来说都更有利。因此我们对上述步骤中的这两步做优化，在对于点云这种比较稠密的数据上，可以这么优化：

选择跨越维度最大的维度，对于点云这种数据来说，这能保证两个子树超平面中包含的点是均匀的。

NOTE
OI-Wiki中的原文是“轮流选择 $k$ 个维度，以保证在任意连续 $k$ 层里每个维度都被切割到。”，我认为也是一种面对数据密度不确定的情况下的一种有效方式。
分割点集时，按照所选的维度上的中位数。这样基本上能保证KD-Tree的树高最多为 $\log n + O(1)$

比如，以三维空间为例：

1
点云数据：
2
P0 = (1.2, 2.3, 1.5)
3
P1 = (5.1, 1.2, 4.8)
4
P2 = (2.5, 5.2, 2.1)
5
P3 = (4.8, 3.5, 3.2)
6
P4 = (0.5, 4.1, 0.8)
7
P5 = (3.2, 2.5, 2.9)
8
P6 = (5.5, 5.5, 5.5)
9
P7 = (1.8, 1.5, 1.2)
10
P8 = (4.2, 4.2, 4.2)
11
P9 = (2.8, 3.8, 3.1)

第一步：选择分割维度：

1
// 选择跨度最大的维度
2
max_span = max(5.0, 4.3, 4.7) = 5.0  ← X维度
3
divfeat = 0  (X坐标)
4
divval = (0.5 + 5.5) / 2 = 3.0

第二步：分割点集：

1
原始点集 (按X坐标)：
2
P0(1.2) P7(1.8) P2(2.5) P9(2.8) P5(3.2) P3(4.8) P1(5.1) P8(4.2) P4(0.5) P6(5.5)
3
                                    ↑
4
                              分割值 = 3.0
5

6
分割后：
7
┌─────────────────┬───────────────┬──────────────────┐
8
│  < 3.0          │   == 3.0      │   > 3.0          │
9
├─────────────────┼───────────────┼──────────────────┤
10
│P0 P7 P2 P9 P4   │  P5           │P3 P1 P8 P6       │
11
│(4个点)          │ (1个点)       │(4个点)           │
12
└─────────────────┴───────────────┴──────────────────┘
13
       ↓                              ↓
14
   左子树                          右子树
15
   继续分割                        继续分割

最终，树的结构：

1
                    ┌─────────────────────────────────────┐
2
                    │ ROOT NODE                           │
3
                    │ divfeat = X (0)                     │
4
                    │ divval = 3.0                        │
5
                    │ children: P0-P9                     │
6
                    └──────────────┬──────────────────────┘
7
                                   │
8
                    ┌──────────────┴──────────────────┐
9
                    ▼                                 ▼
10
            ┌─────────────────┐            ┌──────────────────┐
11
            │ LEFT NODE       │            │ RIGHT NODE       │
12
            │ divfeat = Y(1)  │            │ divfeat = Z(2)   │
13
            │ divval = 2.9    │            │ divval = 4.85    │
14
            └────────┬────────┘            └────────┬─────────┘
15
                     │                              │
16
         ┌───────────┴───────────┐    ┌──────────────┴─────────────┐
17
         ▼                       ▼    ▼                            ▼
18
    ┌────────┐            ┌────────┐  ┌──────┐           ┌──────────────┐
19
    │ LEAF   │            │ LEAF   │  │LEAF  │           │ LEAF         │
20
    │P0 P4   │            │P7 P2   │  │P5 P9 │           │P3 P1 P8 P6   │
21
    │(2 pts) │            │(2 pts) │  │(2pts)│           │(4 points)    │
22
    └────────┘            └────────┘  └──────┘           └──────────────┘

查询#

在点云slam中，最常用的处理方式将来自不同帧的点云进行比较，通过点对点匹配（ICP），点到线（PLICP），面到面（GICP）等loss模型，实现位姿估计；在实时规划方面，也会通过将点云进行分类（动态，静态障碍物），实现实时避障。在这些操作中，存在频繁对数据集中的点进行查询的操作，我们构建KD-Tree来管理点云信息的关键也在这里。

我们知道最基础的对树结构的遍历方式分为深度遍历（Deep First Search）与广度遍历（Breadth First Search）两种，但这两种搜索方式在面对庞大的点数据的KD-Tree上，无法保证高效性。而我们储存的点本身是处于三维有界线性空间的，所以自然存在“范数”这一关键概念，因此我们可以通过点点之间的范数来对树进行剪枝。

对KD-Tree进行查询的主要方式是通过最近邻搜索（k-nearest neighbors algorithm，KNN）的方式实现。

对于要查询的点，我们首先会确认查询点在分割平面的哪一侧，进而有限搜索离查询点更“近”的子树，并以此递归查询：

1
/* 确定查询点在分割平面的哪一侧 */
2
Dimension idx = node->node_type.sub.divfeat;     // 分割维度
3
ElementType val = vec[idx];                      // 查询点在该维度的坐标
4
DistanceType diff = val - node->node_type.sub.divval;
5

6
/* 先搜索closer的子树 */
7
if (diff < 0) {
8
    bestChild = node->child1;    // 左子树离查询点更近
9
    otherChild = node->child2;
10
} else {
11
    bestChild = node->child2;    // 右子树离查询点更近
12
    otherChild = node->child1;
13
}
14

15
/* 先递归搜索最可能包含最近邻的子树 */
16
searchLevel(bestChild, ...);

这种思路被称为最佳有限搜索（Best-First Search），配合之后的剪枝，能大幅度减少搜索的节点数。

当我们查询到某一个子树之前，我们还需要确认这个子树是否具备被查询的“价值”，我们可以通过计算查询点到分割平面的距离，当另一个子树的距离已经超过我们要搜索的最大距离，就没有必要再搜索子树，这大幅度减少了我们递归的层数，减少了空间与时间复杂度（从递归的层面来说，就没有必要将新的函数调用压入系统栈）。

1
/* 计算查询点到分割平面的距离 */
2
cut_dist = distance_.accum_dist(val, divval, idx);
3
// = (val - divval)^2
4

5
/* 当前已找到的K个点中，最远的距离 */
6
DistanceType worst_dist = result_set.worstDist();
7

8
/* 剪枝条件：如果另一个子树的距离已经超过K个候选点的最大距离
9
   就不必搜索它了 */
10
if (mindist + cut_dist > worst_dist) {
11
    // 另一个子树的所有点都不会比当前K个候选更近
12
    // 直接跳过该子树，节省大量计算！
13
    return;
14
}

以上述的树为例，我们的查询过程可以表示为：

1
查询点 P = (3.5, 2.1, 4.8)，K=5
2
    ↓
3
计算初始距离 (P到根节点边界框的距离)
4
    ↓
5
递归搜索
6
    ├─ 比较 P[divfeat] 与分割值
7
    ├─ 选择最可能包含最近邻的子树 (bestChild)
8
    ├─ 递归搜索 bestChild
9
    ├─ 检查是否需要搜索另一个子树 (otherChild)
10
    │   └─ 只有当 |P[divfeat] - divval| < 当前K个候选中最远点的距离
11
    └─ 回溯
12

13
最终返回全局K个最近的点

复杂度分析#

对于树的构建来说，通过边界框计算，树的结构更偏向于平衡树，因此书的空间复杂度为 $O(\log n)$ 。

对于点集 s[n] 来说，KD-Tree 每次进行分割的时候都要求找到中位数，将其置于 s[mid] 处，需要满足 s[l] 都小于 s[mid]，s[r] 都大于 s[mid] 。这样的操作的复杂度是 $O(n)$ 的。因此构建一个KD-Tree的时间复杂度更趋近于 $O(n\log n)$ 。

对于KD-Tree的查询，可以从二维的KD-tree开始考虑。对于二维KD-Tree的一个节点来说，其有四个孙子节点，且它到每一个孙子都在两个维度上各进行了一次划分。按照这种方法将一个矩形划分成四个子矩形，一条与坐标轴平行的线段最多经过两个区域，即从 𝑢 [u] 出发的查询，最多向下进入两个孙子，由于建树的时候，子树在当前划分维度的中位数，所以子树大小必定减半。于是假设该节点的的子树的大小是 $n$ ，那么就有如下的递推式：

T(n) = 2 T(n / 4) + O(1)

由Master定理可得 $T(n) = O(\sqrt{n})$ 。

推广到 $k$ 维，可得： $T(n) = 2^{k-1} T(n/2^k) + O (1)$ ，于是可得：

T(n) = O(n^{1-1/k})