1533 字

8 分钟

【算法】基础算法模板

2025-11-12

Algorithm

/

C++

基础算法模板#

TIP
Keep on updating…

Mater Theorem#

主定理（Master Theorem）是分析递归法复杂度的重要定理。

Master 公式如下：

T(n) = a * T(n/b) + O(n^c),\ \text{where a,b,c is const}

如果 $\log(b,a) < c$ , 那么复杂度为： $O(n^c)$
如果 $\log(b,a) > c$ , 那么复杂度为： $O(n^{\log(b,a)})$
如果 $\log(b,a) = c$ , 那么复杂度为： $O(n^c * \log n)$

addtion: $T(n) = 2 * T(n/2) + O(n *\log n)$ 的时间复杂度为 $O(n * ((\log n)^2))$

二分查找#

1
// find max idx of num <= tar
2
int binary_search() {
3
  int ans = -1;
4
  while (l <= r) {
5
    int m = l + ((r - 1) >> 2);   // avoid memory overflow
6
    if (Array[m] >= tar) {
7
      r = m - 1;
8
      ans = m;
9
    }
10
    if (Array[m] < tar) {
11
      l = m + 1;
12
    }
13
  }
14

15
  return ans;
16

17
}

树的遍历#

树的前序，中序，后序遍历

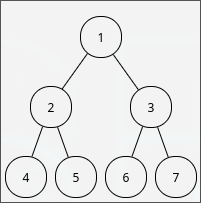
以下图中的树为例

example tree

先序：中，左，右

期望输出：
```
1
1 2 4 5 3 6 7
```
中序：左，中，右

期望输出：
```
1
4 2 5 1 6 3 7
```
后序：左，右，中

期望输出：
```
1
4 5 2 6 7 3 1
```

递归版#

前序遍历：

1
void printPreorder(treeNode *root) {
2
  if (root == nullptr)
3
    return;
4

5
  cout << root->val << " ";
6
  printPreorder(root->left);
7
  printPreorder(root->right);
8
}

中序遍历：

1
void printInorder(treeNode *root) {
2
  if (root == nullptr)
3
    return;
4

5
  printInorder(root->left);
6
  cout << root->val << " ";
7
  printInorder(root->right);
8
}

后序遍历：

1
void printPostorder(treeNode *root) {
2
  if (root == nullptr)
3
    return;
4

5
  printPostorder(root->left);
6
  printPostorder(root->right);
7
  cout << root->val << " ";
8
}

栈实现版#

NOTE
递归法的实现依赖于语言底层实现的系统栈。会将当前没有运行完毕的函数压入系统栈（递归序）。
使用栈的方式实现树的遍历，本质上就是使用内存栈代替系统栈。可以通过理解系统栈的运行机制来实现通过内存栈来代替系统栈。节点入栈等同于将未处理的节点进行记录，通过之后的出栈pop操作再重新处理该节点。
同时还有一个小技巧，上述的“处理节点”，等同于“处理以节点为根节点的子树”。

对于前序遍历，使用栈实现的步骤如下：

打印栈顶元素，栈中弹出
如果右节点不为空，压入右节点
如果左节点不为空，压入左节点
重复1,2,3直到栈为空

代码如下：

1
void printPreorder_stack(treeNode *root) {
2
  if (!root)
3
    return;
4

5
  std::stack<treeNode> st;
6
  st.push(*root);
7
  while (!st.empty()) {
8
    treeNode tmp = st.top();
9
    cout << tmp.val << " ";
10
    st.pop();
11
    if (tmp.right)
12
      st.push(*tmp.right);
13
    if (tmp.left)
14
      st.push(*tmp.left);
15
  }
16
  return;
17
}

NOTE
在前序遍历中，我们会先优先处理栈顶元素，之后在考虑将栈顶元素的左右节点入栈

对于中序遍历，使用栈实现步骤如下：

子树左边界进栈，直到左边界为空
栈中弹出节点，打印，节点右树重复 1
直到没有子树，且栈为空

代码如下：

1
void printInorder_stack(treeNode *root) {
2
  if (!root)
3
    return;
4

5
  std::stack<treeNode> st;
6
  treeNode *head = root; // 认为是子树的头节点
7
  while (!st.empty() || head != nullptr) {
8
    if (head) {
9
      st.push(*head);
10
      head = head->left;
11
    } else {
12
      head = &st.top();
13
      st.pop();
14
      cout << head->val << " ";
15
      head = head->right;
16
    }
17
  }
18
}

NOTE
在中序遍历中，我们会先找到树最深的左节点。通过head指针，可以标记当前正在处理的子树

对于后序遍历，有两种实现方式：两个栈版，一个栈版。前者比较好理解，所以将两种版本都放在这里进行参考：

两个栈版：

先序为中，左，右。很自然能联想到先’序：中，右，左（上述代码中的压入顺序调整一下即可），那么后序就是将先’序倒置，只需要使用另一个栈收集先’的输出，最后将这个收集栈打印出来即可

将栈顶元素收集到收集栈，弹出
左节点存在，入栈
右节点存在，入栈
重复1,2,3直到栈空

代码如下：

1
void printPostorder_twoStack(treeNode *root) {
2
  if (!root)
3
    return;
4

5
  std::stack<treeNode> st;
6
  std::stack<treeNode> collect;
7
  st.push(*root);
8
  while (!st.empty()) {
9
    treeNode tmp = st.top();
10
    collect.push(tmp);
11
    st.pop();
12
    if (tmp.left) {
13
      st.push(*tmp.left);
14
    }
15
    if (tmp.right) {
16
      st.push(*tmp.right);
17
    }
18
  }
19

20
  while (!collect.empty()) {
21
    cout << collect.top().val << " ";
22
    collect.pop();
23
  }
24
}

一个栈版本：

初始化指针 head 指向头节点，cur 指向当前遍历节点，根节点入栈
判断左树是否处理过，没有处理入栈
判断右树是否处理过，没有处理入栈
左右树都处理过了，则打印当前节点，head指向栈顶，重复2,3

代码如下：

1
void printPostorder_sigStack(treeNode *root) {
2
  if (!root)
3
    return;
4

5
  std::stack<treeNode *> st;
6
  st.push(root);
7
  treeNode *head = root;
8
  while (!st.empty()) {
9
    treeNode *cur = st.top();
10
    if (cur->left != nullptr && head != cur->left && head != cur->right) {
11
      st.push(cur->left);
12
    } else if (cur->right != nullptr && head != cur->right) {
13
      st.push(cur->right);
14
    } else {
15
      cout << cur->val << " ";
16
      head = st.top();
17
      st.pop();
18
    }
19
  }
20
}

NOTE
后序遍历与中序遍历相似的地方是，后序遍历也需要先找到最深的根。不同的是中序遍历是找到最深的子树之后，回到根节点，但后序遍历需要先完全处理cur为根节点的子树。因此使用head标记已经处理完的子树，按照先左后右的顺序处理深层的子树。

排序#

归并排序#

归并排序是归并思想在排序上的应用。将排序的复杂度降到了 $O(n\log n)$

排序的主要思想：

将问题从中点拆分
通过merge合并两部分的结果

以5个数的归并排序为例，可以将问题划分成如下图所示：

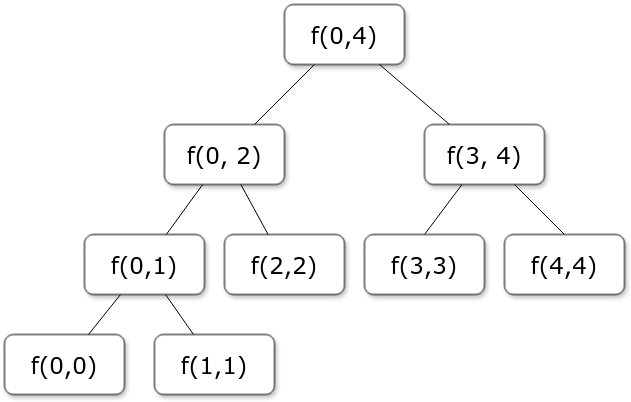
归并排序实例

可以看到在划分的最后，节点已经不能再划分，只能向上执行merge操作

归并排序完整代码：

1
#include <iostream>
2

3
using namespace std;
4

5
const int N = 10001;
6
int n;
7
int arr[N];
8
int tmp[N];
9

10
void merge(int l, int m, int r) {
11
  int lp = l;
12
  int rp = m + 1;
13
  int begin = 0;
14
  while (lp <= m && rp <= r) {
15
    tmp[begin++] = arr[lp] > arr[rp] ? arr[rp++] : arr[lp++];
16
  }
17

18
  while (rp <= r) {
19
    tmp[begin++] = arr[rp++];
20
  }
21
  while (lp <= m) {
22
    tmp[begin++] = arr[lp++];
23
  }
24

25
  for (int i = 0; i < begin; i++) {
26
    arr[l + i] = tmp[i];
27
  }
28
}
29

30
void merge_sort(int l, int r) {
31
  if (l >= r)
32
    return;
33

34
  int m = (l + r) >> 1;
35
  merge_sort(l, m);
36
  merge_sort(m + 1, r);
37

38
  merge(l, m, r);
39
}
40

41
int main() {
42
  cin >> n;
43
  for (int i = 0; i < n; i++) {
44
    int val;
45
    cin >> val;
46
    arr[i] = val;
47
  }
48

49
  merge_sort(0, n - 1);
50
  for (int i = 0; i < n; i++) {
51
    cout << arr[i] << " ";
52
  }
53

54
  return 0;
55
}